Mittlerweile kennen wir sie alle nur zu gut – die gefürchtete Exponentialfunktion und die ersehnte Glockenkurve. Sie veranschaulichen die Anzahl der auf Sars-CoV-2 positiv getesteten Personen – je nachdem, ob man die Verbreitung des Virus unter Kontrolle bekommt oder nicht.
Die Exponentialfunktion ist eine der wichtigsten Funktionen in der angewandten Mathematik. Sie beschreibt einen Prozess, bei welchem eine Größe proportional zu ihrer Menge wächst. Das heißt, je größer die Menge, desto größer das Wachstum – jene Eigenschaft, die Wissenschafterinnen, Wissenschafter, Politikerinnen und Politiker hochgradig nervös macht. Exponentielles Wachstum kann man häufig in der Natur beobachten, zum Beispiel beim Wachstum von Bakterien oder dem radioaktiven Zerfall von Atomen. Die klassische Glockenkurve ist auch eine Exponentialfunktion – nur hat sie anstatt einer positiven Wachstumsrate eine negative. Sie steigt erst an, um dann abzuflachen und wieder abzufallen. Und somit bewahrheitet sich die alte mathematische Weisheit: Aufs Vorzeichen kommt's an.
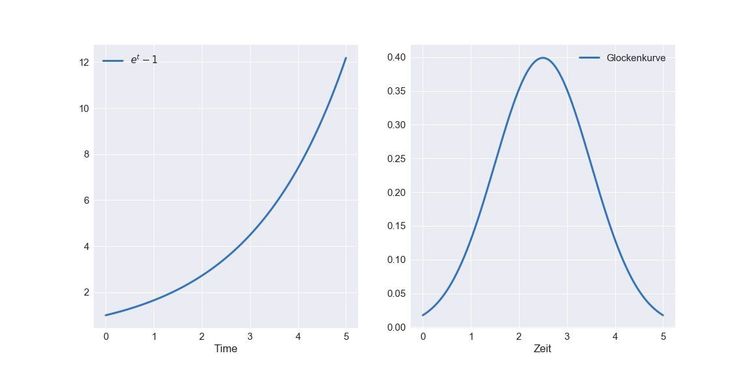
Rechts: Glockenkurve.
Der mögliche weitere Verlauf der Covid-19-Fallzahlen wurde – basierend auf verschiedenen Szenarien – prognostiziert. Diese Prognosen beruhen auf mathematischen epidemiologischen Modellen, welche die Verbreitung des Virus in einer Gesellschaft beschreiben. Sowohl die Exponentialfunktion als auch verschiedene Arten von Glockenkurven können Lösungen solcher epidemiologischer Modelle sein – je nachdem, welche Parameter und Situationen man wählt.
SIR-Modell
Die meisten verwendeten Modelle basieren auf den folgenden Annahmen: Eine Person ist entweder für das Virus empfänglich (susceptible), infiziert (infected) oder genesen (recovered) beziehungsweise tot. Hat man die Krankheit überstanden, wird man meist als immun angesehen und kann das Virus nicht weiterverbreiten. Dieses einfachste mathematische Modell – das sogenannte SIR-Modell – kann dann weiter verfeinert werden. Zum Beispiel indem man weitere Kategorien, etwa asymptomatisch infiziert und nicht erkannt, hinzufügt. Auch werden die jeweiligen Gruppen in den verschiedenen Kategorien oft noch weiter unterteilt, etwa nach Alter und Geschlecht. So kann dann die Wahrscheinlichkeit einer Ansteckung, also die Zahl jener Personen, die sich in einem bestimmten Zeitraum infizieren, für verschiedene Gruppen – basierend auf weiteren Informationen wie Kontakt- und Mobilitätsdaten – adjustiert werden.
Die Parameter Beta und Gamma stehen im Verhältnis zur Anzahl neuer Infektionen und der Gesundungs- und Sterberate der infizierten Personen. Die allgemeine Sterbe- und Geburtenrate pro Person wird durch die Parameter Mu und Nu inkludiert.
Durch diese Unterteilungen und die zusätzlichen Informationen werden die Modelle aber auch immer komplexer – und damit steigt die Anzahl der zugrundeliegenden Annahmen und Parameter. Viele dieser Annahmen sind jedoch nicht validiert, und es ist auch nicht immer möglich, Parameter zu schätzen oder die Ausgangslage konkret anzugeben (wie viele Personen sind aktuelle infiziert?). Oft werden daher auch stochastische Komponenten, das heißt, Unsicherheiten in der Modellierung wie auch bei den Parametern, inkludiert. Wie sich diese Unsicherheiten auf das Ergebnis auswirken, die sogenannte "uncertainty quantification", ist ein wichtiges mathematische Forschungsgebiet. Sind die Modelle simpel genug, kann man die Größenordnung des Fehlers oft quantifizieren. Doch je komplexer die Modelle werden, desto schwieriger ist es, verlässliche Aussagen zu treffen.
Methode der Wahl
Des Weiteren werden SIR-Modelle (und deren vielfältige Varianten) in gleichungsbasierte oder agentenbasierte Modelle unterteilt. Im ersten Fall unterscheidet man nur die jeweiligen S-, I- und R-Gruppen (und deren Unterteilungen in Alter, Geschlecht et cetera), während man im agentenbasierten Modell jede Person einzeln beschreibt. Diese Modelle sind daher noch detaillierter und komplexer, da Ergebnisse und Vorhersagen auf zahlreichen systematischen Computersimulationen basieren. Der Vorteil von gleichungsbasierten SIR-Modellen ist deren einfachere Form. Sie erlaubt Mathematikern Lösungen beziehungsweise den Einfluss von Faktoren, etwa die Ansteckungswahrscheinlichkeit, zu analysieren. Dabei kommt unweigerlich die Frage auf, welches Modell denn das richtige ist.
Das hängt einmal von der Fragestellung ab. Will man zum Beispiel den Effekt gezielter Maßnahmen, das heißt, den Einfluss einzelner Parameter im Modell, auf die Gesamtpopulation testen, sind gleichungsbasierte Modelle die Methode der Wahl. Will man Prognosen treffen, sind agentenbasierte Modelle in Kombination mit empirischen Daten sicher aussagekräftiger.
Wie viele Kontakte haben Personen?
Aber gerade die benötigten Informationen über unser individuelles Verhalten sind nur sehr bedingt vorhanden, auch weil wir diese verständlicherweise nicht einfach so teilen wollen. Kollegen in England haben erst kürzlich die Daten von 36.000 Freiwilligen im Zuge des "BBC Pandemic Experiment" analysiert, um herauszufinden, wie viele Kontakte Personen innerhalb und außerhalb ihrer eigenen Altersgruppe haben. Dies ist gerade für die älteren, besonders gefährdeten Altersgruppen wichtig. Die Daten zeigten, dass es eine Affinität für die eigene Altersgruppe gibt, 30- bis 35-Jährige die meisten Kontakte haben und sich die Präferenz für die eigene Altersgruppe im höheren Alter verliert.
Ein weiterer Unsicherheitsfaktor sind die tatsächlichen Fallzahlen. Diese kann man mit Vorhersagen mathematischer Modelle vergleichen. Das ist allerdings aufgrund der weiterhin geringen Anzahl an Testungen auch nur bedingt aussagekräftig. Wie derzeitige Tests effizienter organisiert werden können, haben drei Wiener Mathematiker schon im STANDARD erläutert.
Und so sieht man, dass es weiterhin viele Unsicherheiten und Fragen gibt, die verlässliche Prognosen schwierig machen. Zwar werden mathematische Modelle und Methoden in Zukunft eine wichtige Rolle spielen, um die Pandemie in den Griff zu bekommen. Aber bis wir das alles überstanden haben, ist es wahrscheinlich noch ein langer Weg. Bis dahin: Take care and stay sane. (Marie-Therese Wolfram, 8.5.2020)