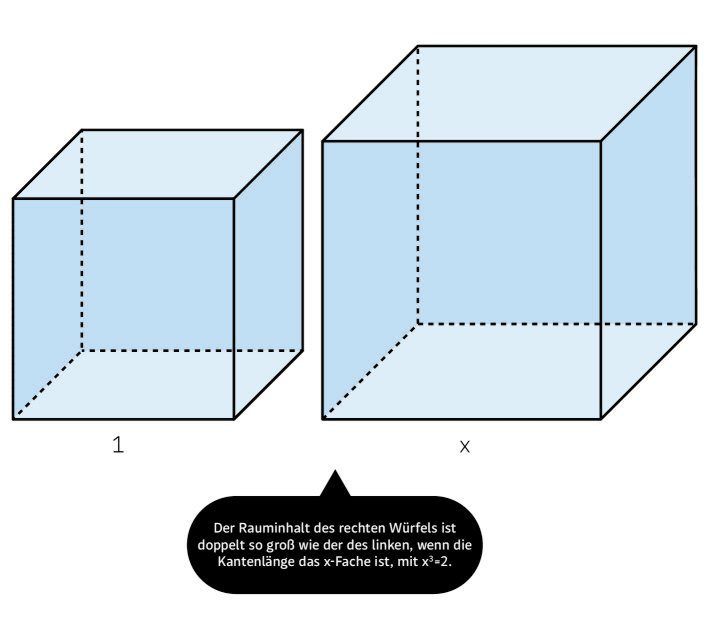
Der Rauminhalt des rechten Würfels ist doppelt so groß wie der des linken, wenn die Kantenlänge das x-Fache ist, mit x3 = 2.

Erst gab’s den Internationalen Tag der Arbeit, dann den Muttertag, dann den Tag der Menschenrechte und den Weltmurmeltiertag. Seit 2020 gibt es auch den Internationalen Tag der Mathematik, kurz p-Tag genannt, und zwar am 14. 3. (denn die Kreiszahl p ist 3,14…). Großes war damals geplant. Stattdessen kam ein Lockdown. Auch heuer gibt es keine rauschenden Feiern. Corona lähmt alles.
Wer Trost sucht, findet ihn in der Geschichte. Denn mindestens zweimal hat eine Pandemie den Anstoß gegeben für einen epochalen mathematischen Fortschritt. Im Jahr 430 vor unserer Zeitrechnung ging es um die Würfelverdoppelung und Anno Domini 1665 um die Infinitesimalrechnung.
Die attische Pest wütete während der Blütezeit der griechischen Kultur. Perikles war ihr prominentestes Opfer. Noch jetzt stößt man auf Massengräber von damals, doch erlauben sie nicht, die Krankheit näher zu bestimmen. In jener Zeit hieß jede Seuche "Pest".
Die Götter mögen es doppelt
Schon damals gab es Experten, die genau wussten, was zu tun war. Auf der Insel Delos befragte man das Orakel. Die Antwort: Der würfelförmige Altar des Apollo-Tempels müsse verdoppelt werden. Ein doppelt so großer Würfel, und schon wären die Götter befriedigt und die Pest besiegt.
Irgendwann, nach einer zweiten oder dritten Welle, war die attische Pest dann tatsächlich vorbei. Der Tempel verfiel. Der Altar ist verschwunden. Was blieb, war das Delische Problem: die Würfelverdoppelung.
Wieso Problem? – Nun, das Volumen muss verdoppelt werden. Man kann dazu nicht einfach einen Würfel von doppelter Kantenlänge verwenden. Dann hätte man nämlich das Volumen verachtfacht, nicht verdoppelt. Man muss die Kantenlänge um einen Faktor x vergrößern, und zwar so, dass x3 = 2 gilt. Dieses x, die kubische Wurzel von 2, ist ungefähr 1,26… Doch die alten Griechen mochten sich nicht mit einem "ungefähr" begnügen. Sie brauchten den genauen Wert. Sie wollten dieses ominöse x mit Zirkel und Lineal konstruieren. Die Götter, so viel war ja bekannt, treiben Geometrie, und in dieser Branche gilt es, exakt zu sein.
Frage-und-Antwort-Spiel
Es stellte sich bald heraus, dass die Aufgabe schwierig war. Das war umso irritierender, als ein ganz ähnliches Problem sehr leicht zu lösen ist: nämlich ein vorgegebenes Quadrat zu verdoppeln. Diese Aufgabe ist so simpel, dass sie sogar Philosophen zugemutet werden kann. Sie kommt in einer frühen Schrift von Plato vor.

Der Dialog "Menon", eigentlich ein Theaterstück, spielt dreißig Jahre nach der attischen Pest. Die Hauptrolle übernimmt Sokrates. Er hat die Seuche überlebt und nähert sich dem Pensionsalter. Jetzt will er Menon, einem Politabenteurer, erklären, woher unser Wissen stammt: nämlich aus der Erinnerung.
Um das zu beweisen, befragt Sokrates einen jungen Sklaven aus dem Haushalt seines Gastgebers, einen Knaben, der bestimmt nie Geometrie gelernt hat. Erst erklärt ihm Sokrates, was ein Quadrat ist. Dann die Frage: Wie man es verdoppeln könne? – Nun, doppelt so lange Seiten, natürlich. – Aber nein, das gäbe ja ein viermal so großes Quadrat. – Ach so. Also dann wohl anderthalb mal so lange Kanten. – Nein, auch nicht. Und so weiter. Im Zug des Frage-und-Antwort-Spiels bringt Sokrates den Sklavenjungen zur Einsicht, dass die Diagonale des ursprünglichen Quadrats als Seite eines verdoppelten Quadrats dienen kann.
Der Versuch ist beendet, und der Sklave taucht zurück in seine bildungsferne Schicht, ohne zu ahnen, dass er im Verlauf einer Viertelstunde berühmt geworden ist – wenngleich sein Name unerwähnt blieb. Sokrates aber erklärt dem Menon, dass der Junge das Quadratverdoppeln offenbar schon gekannt haben muss – es wurde ihm ja nie gelehrt. Unzweifelhaft habe er sich an etwas erinnert, das er bereits wusste. Anamnese, was sonst.
Die Kunst, sich das Leben schwer zu machen
Um das Quadrat zu verdoppeln, muss man die Seiten um einen Faktor x strecken, sodass x2 = 2 ist. Dieses x ist die Quadratwurzel von 2, ungefähr 1,42… Wieder ein "ungefähr", aber diesmal ist die Länge leicht zu konstruieren. Man kann sie abtragen mit dem Zirkel. Es ist die Diagonale des Quadrats mit Seitenlänge 1. Wenn die Verdoppelung des Quadrats so leicht geht, warum macht dann das Verdoppeln des Würfels Probleme?
Mehr als zweitausend Jahre lang blieb das sogenannte Delische Problem ungelöst, obwohl sich viele Mathematiker damit herumschlugen, und auch begabte Amateure wie Casanova oder Napoleon. Zwei andere geometrische Probleme erwiesen sich als ebenso widerborstig. Eines ist die Winkeldreiteilung: Bei manchen Winkeln (etwa bei 90 Grad) geht es ganz leicht, sie zu dritteln, aber bei den meisten (etwa bei 60 Grad) kommt man auf keinen grünen Zweig.
Das andere Problem ist die Quadratur des Kreises. Der Name wurde zum Synonym für eine unlösbare Aufgabe: Für einen gegebenen Kreis konstruiere man das Quadrat mit demselben Flächeninhalt. Dabei zu beachten ist, dass nur Zirkel und Lineal verwendet werden dürfen, keine komplizierteren Geräte. Die überließ man den Handwerkern. Eine Art Reinheitsgebot schrieb vor: Man darf durch vorgegebene zwei Punkte eine Gerade ziehen. Man darf einen Kreis ziehen mit vorgegebenem Mittelpunkt und Radius. Und sonst darf man gar nichts!
So kann man neue Punkte aus den gegebenen konstruieren, aber nur als Schnittpunkt von zwei Geraden oder einer Geraden und einem Kreis oder von zwei Kreisen. Diese neuen Punkte kann man wiederum verwenden, um daraus weitere zu konstruieren, und so fort. Alles andere verletzt die Spielregeln. Diese Selbstbeschränkung der griechischen Geometer macht ihre berüchtigten drei Probleme so schwer.
Erweiterungen und wo sie nicht hinführen
Ein Fortschritt wurde erst ermöglicht durch einen Nachfolger des Sokrates, den Philosophen René Descartes. Der lag auf seinem Bett und kogitierte, wie so oft. Eine Fliege kroch über die Zimmerdecke. Descartes bemerkte, dass man die Position der Fliege durch zwei Zahlen bestimmen kann, den Abständen zu den Kanten des Plafonds. Die kartesischen Koordinaten waren geboren. Zum Glück war Descartes nicht kurzsichtig, sonst hätte er die Fliege über seinem Kopf nicht bemerkt. So aber kamen die Zahlen in die Geometrie und mit den Zahlen die Algebra – eine Wissenschaft, die den alten Griechen fremd war.
Einen Punkt "mit Zirkel und Lineal" zu konstruieren: in Koordinaten bedeutet das, lineare oder quadratische Gleichungen zu lösen, also ax + b = 0 oder x2 + ax + b = 0, zu gegebenen a und b. Dazu braucht man weiter nichts als die vier Grundrechnungsarten (Addition, Subtraktion, Multiplikation und Division) und das Ziehen von Quadratwurzeln. Die geometrischen Konstruktionsaufgaben erfordern oft Zwischenschritte, also das Bestimmen von Hilfspunkten. Das bedeutet, die entsprechenden Koordinaten aus den bereits gegebenen zu "konstruieren", Schritt für Schritt.
Bruchzahl konstruieren
Hat man etwa auf der Zahlengeraden 0 und 1 gegeben, so kann man mit Zirkel und Lineal jede Bruchzahl konstruieren. Das liefert den Bereich der rationalen Zahlen. Auf die kann man nach Herzenslust die vier Grundrechnungsarten anwenden (außer durch 0 dividieren) und kommt doch nie aus dem Bereich heraus. Man kann auch jede Quadratwurzel konstruieren. Doch die Quadratwurzel von 2 beispielsweise ist keine rationale Zahl. Man hat den Bereich verlassen.
Ein größerer Bereich tut sich auf: Er besteht aus der Wurzel von 2, den rationalen Zahlen und allem, was man durch die Grundrechnungsarten daraus erhält. Doch wieder kann die Konstruktion einer Quadratwurzel aus diesem Bereich hinausführen. Man erhält so einen weiteren Bereich. Das kann man so oft wiederholen, wie man will, und erhält solcherart alle konstruierbaren Zahlen.

Im Jahr 1837 bewies der dreiundzwanzigjährige Franzose Pierre Wantzel, dass die Lösung von x3 = 2 keine konstruierbare Zahl ist. Das bedeutet, dass das Delische Problem unlösbar ist. Es ist nicht nur äußerst schwierig, nicht nur ungelöst: Es kann unmöglich gelöst werden! Dasselbe gilt für die Dreiteilung des Winkels von 60 Grad – auch das bewies Wantzel. Und dasselbe gilt auch für die Quadratur des Kreises, was allerdings erst später bewiesen wurde. Wantzel erlebte es nicht mehr. Er starb früh, wenig beachtet. Die Nachwelt einigte sich darauf, den Löwenanteil am Ergebnis dem großen Carl Friedrich Gauß zuzuschreiben.
Der Nachweis der Unlösbarkeit der Würfelverdoppelung ist eine der wichtigsten Etappen in der Entwicklung der Mathematik. Man darf getrost sagen: Könnte man den Würfel mit Zirkel und Lineal verdoppeln, wäre es kaum der Rede wert. Eine gelöste Geometrieaufgabe mehr, eine unter tausenden! Aber eben weil das Problem allen Lösungsversuchen widerstand, lenkte es die Mathematik in neue Bereiche. Dass man den Würfel nicht verdoppeln kann, ist somit alles andere als ein negatives Resultat. Es lieferte eine tragende Säule der Mathematik: die Theorie der Körpererweiterungen.
Annus mirabilis in Quarantäne
1665: Mehr als zweitausend Jahre nach der attischen Pest verheerte die "große Pest" England. Die Londoner flohen in Scharen. Die Universitäten schlossen. Ein Student aus Cambridge namens Isaac Newton, der gerade seinen Bachelor gemacht hatte, ohne groß aufzufallen, zog sich in sein Heimatdorf zurück. Der Mastergrad musste warten. Onlineprüfungen gab es nicht.
Der Rest ist Geschichte. In Selbstisolation, einen Apfelbaum vor dem Fenster und die "Geometrie" des Descartes auf dem Tisch, revolutionierte Newton Mathematik, Physik und Astronomie. Als er zwei Jahre später nach Cambridge zurückkehrte, war sein Studienabschluss nur noch Formsache. Mit 28 Jahren übernahm Newton die bedeutendste Lehrkanzel Englands.
Newton berichtet wenig darüber, wie er zu seinen Entdeckungen gelangt ist (außer dass er dabei immer allen anderen zuvorgekommen sei, insbesondere jenem hinterhältigen Gottfried Wilhelm Leibniz). Er hatte seine großen Themen schon vorher gefunden, und sie ließen ihn auch nachher nicht los: Optik, Schwerkraft, Himmelsmechanik und die Infinitesimalrechnung, also das Rechnen mit unendlich kleinen Größen (das Differenzieren und Integrieren). Es könnte Zufall sein, dass Newtons Annus mirabilis mit seiner Quarantäne zusammenfiel. Aber offenbar haben dem jungen Newton weder seine Professoren gefehlt, noch hat ihn das "social distancing" behindert. Das wird den Studierenden von heute freilich kein Trost sein.
Das Genie als Hexenmeister
Die Welt von damals war unfassbar anders. Wir kennen Newton als genialen Begründer des modernen wissenschaftlichen Weltbilds. Dass er Astrologe, Alchemist und Sonderling war, verdrängt die Nachwelt gern. Seine "Principia Mathematica" sind zum Klassiker geworden. Er hat aber auch ganz andere Schriften hinterlassen, etwa zu Thema Pest. Da wirkt er wie ein Hexenmeister aus "Harry Potter".
Vergangenen Juni wurde ein Manuskript von Newton versteigert, in welchem er Mittel gegen die Pest beschreibt. "Am besten ist es, eine Kröte drei Tage lang an den Beinen über einem Kamin aufzuhängen, bis sie speit und stirbt." Dann müsse man nur noch die Kröte zerstampfen, mit ihrem Erbrochenen mischen und daraus eine Tablette anfertigen, die aufs Pestgeschwür appliziert wird. – Man möchte weder Kröte noch Patient sein.
Newton ist nicht als Arzt berühmt geworden. Das Rezept wurde in keine "Gesammelten Werke" aufgenommen. Doch beleuchtet es den zeitgenössischen Hintergrund von Aberglauben, Höllenangst und Seuchenspuk. In diesem Licht scheint Newtons Infinitesimalrechnung umso erstaunlicher. Der Hexer rechnete mit dem "unendlich Kleinen", das es doch eigentlich gar nicht geben kann, und wusste jeden falschen Schritt mit der Sicherheit eines Schlafwandlers zu vermeiden. (Karl Sigmund, 14.3.2021)
Archimedes verletzt die Spielregeln

Das Schlagwort "Nur Zirkel und Lineal" gibt das Reinheitsgebot nicht ganz korrekt wieder. So ist es beispielsweise auch verboten, zwei Punkte A und B auf dem Lineal zu markieren und dieses Lineal dann so zu bewegen, dass A stets auf einer vorgegebenen Geraden und B stets auf einem vorgegebenen Kreis liegt, bis schließlich das Lineal durch einen vorgegebenen Punkt geht. Obwohl hier nur das Lineal verwendet wird, ist die Konstruktion unerlaubt. Das hat Archimedes nicht davon abgehalten, mit diesem Trick Winkel zu dritteln. Nämlich so:
Gegeben sei der rote Winkel mit Scheitelpunkt O. Ein beliebiger Kreis mit Mittelpunkt O schneidet die Schenkel des Winkels in P und Q. Man markiere zwei Punkte A und B auf dem Lineal, sodass ihr Abstand gleich dem Kreisradius OQ ist. Man verlängere OP zu einer Geraden g. Man bewege jetzt das Lineal so, dass stets A auf der Geraden g liegt und B auf dem Kreis. Irgendwann liegt auch Q auf dem Lineal. Dann zeichne man die neue Gerade h, auf der nun A, B und Q liegen. Der Winkel x zwischen g und h ist genau ein Drittel des roten Winkels. Wieso? (Hinweis: OB ist so lang wie AB; der Winkel in Q ist doppelt so groß wie der Winkel in A.)
Wie man schmerzlos Wurzeln zieht

Wenn auf einer Geraden die Strecken AB und BC liegen, dann konstruiere man die Senkrechte auf die Gerade durch B, und den Kreis mit Durchmesser AC (geht alles mit Zirkel und Lineal). Der Kreis schneidet die Senkrechte in einem Punkt D. Wenn die Strecke BD die Länge x hat und AB und BC die Längen a und 1, dann ist x die Quadratwurzel von a. Wieso? (Hinweis: Der Winkel ADC ist ein rechter Winkel; die Dreiecke ABD und DBC sind einander ähnlich.)
Die Quadratur des Kreises rollt wie von selbst ab

Gegeben sei der rote Kreis mit Radius R und Inhalt pR2. Er berührt eine Gerade im Punkt A. Wir lassen ihn auf dieser Geraden abrollen. Nach einer halben Umdrehung berührt er die Gerade im Punkt B, um einen halben Kreisumfang, also pR, von A entfernt. Wir ziehen durch B die Senkrechte zur Geraden. Den Halbkreis durch A, der seinen Mittelpunkt auf der Geraden hat und den Durchmesser pR + R besitzt, schneidet die Senkrechte im Punkt C. Das grüne Quadrat mit der Kante BC hat den Flächeninhalt pR2, wie der rote Kreis. Wieso? (Hinweis: Dieselbe Überlegung wie im vorigen Beispiel zeigt, dass die Länge BC gleich R mal der quadratischen Wurzel von p ist. Das Quadrat hat also denselben Flächeninhalt wie der Kreis.)